机器学习之朴素贝叶斯算法（下）

1. 条件独立性

两个随机变量X和Y，若对于所有x，y有P(X=x，Y=y)=P(X=x)P(Y=y)则称随机变量和是相互独立的，记作X⊥Y。

如果关于X和Y的条件概率对于Z的每一个值有P(X=x，Y=y|Z=z)=P(X=x|Z=z)P(Y=y|Z=z)，

则称随机变量X和Y在给定随机变量Z时是条件独立的，记作X⊥Y|Z。

2. 贝叶斯定理

贝叶斯定理是关于随机事件A和B的条件概率（或边缘概率）的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。

3. 朴素贝叶斯算法

基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布，然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率较大的输出y。根据贝叶斯定理，对一个分类问题，给定样本特征X，样本属于类别H的概率是

P(H│X)=(P(X|H)P(H))/(P(X))

其中，是数据元组，通常用个属性集的测量值描述。为某种假设，如数据元组属于某个特定类。(│) 是后验概率，或在条件下，的后验概率。()是先验概率，或的先验概率，()独立于。()是的先验概率。

因为朴素的假设，即特征条件独立，根据全概率公式展开，得出朴素贝叶斯法分类的基本公式：

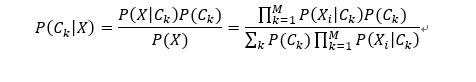
4. 朴素贝叶斯实例

4.1. 实例描述

训练集统计结果(指定统计词频)：

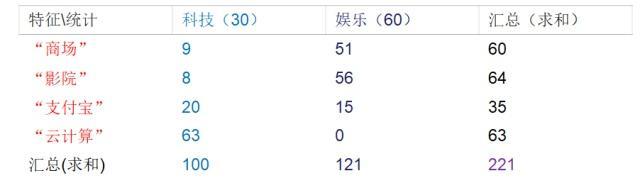
现有一篇被预测文档：出现了影院，支付宝，云计算，计算属于科技、娱乐的类别概率？

4.2. 实例公式

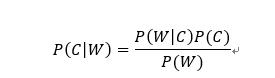
注：w为给定文档的特征值(频数统计,预测文档提供)，c为文档类别

公式可以理解为：

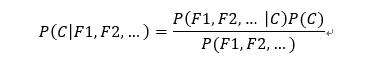
其中c可以是不同类别

公式分为三个部分：

l P(C)：每个文档类别的概率(某类别文档数/总文档数)

l P(W|C)：给定类别下特征(被预测文档中出现的词)的概率

计算方法：P(F1│C)=Ni/N（训练文档中去计算）

Ni为该F1词在C类别所有文档中出现的次数

N为所属类别C下的文档所有词出现的次数和

l P(F1,F2,…) 预测文档中每个词的概率

4.3. 分析的结果

​

5. 拉普拉斯平滑系数

问题：从上面的例子我们得到娱乐概率为0，这是不合理的，如果词频列表里面有很多出现次数都为0，很可能计算结果都为零

解决方法：拉普拉斯平滑系数

P(F1│C)=(Ni+α)/(N+αm)

α为指定的系数一般为1，m为训练文档中统计出的特征词个数

6. 朴素贝叶斯算法案例

6.1. 案例描述-实现新闻分类

sklearn20类新闻分类

20个新闻组数据集包含20个主题的18000个新闻组帖子

6.2. 案例开发流程

1、加载20类新闻数据，并进行分割

2、生成文章特征词

3、朴素贝叶斯estimator流程进行预估

6.3. 代码实现

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
def naviebayes():
    """
    朴素贝叶斯进行文本分类
    :return: None
    """
    news = fetch_20newsgroups(subset='all')
    # 进行数据分割
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
    # 对数据集进行特征抽取
    tf = TfidfVectorizer()
    # 以训练集当中的词的列表进行每篇文章重要性统计['a','b','c','d']
    x_train = tf.fit_transform(x_train)
    print(tf.get_feature_names())
    x_test = tf.transform(x_test)
    # 进行朴素贝叶斯算法的预测
    mlt = MultinomialNB(alpha=1.0)
    print(x_train.toarray())
    mlt.fit(x_train, y_train)
    y_predict = mlt.predict(x_test)
    print("预测的文章类别为：", y_predict)
    # 得出准确率
    print("准确率为：", mlt.score(x_test, y_test))
    print("每个类别的精确率和召回率：", classification_report(y_test, y_predict, target_names=news.target_names))
    return None
if __name__ == "__main__":
    naviebayes()​

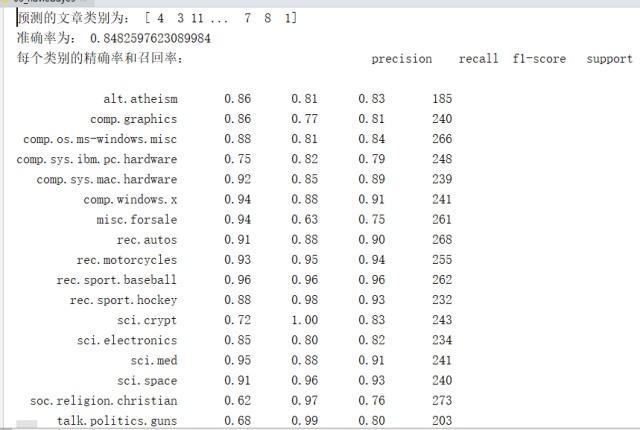
6.4. 案例结果