平均值，方差，标准差

　　均值

​

　　均值描述的是样本集合的中间点，它告诉我们的信息是有限的。

　　方差

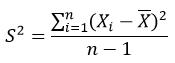
　　方差（variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是各个数据分别与其平均数之差的平方的和的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。方差是衡量源数据和期望值相差的度量值。

　　例如：

　　方差是指一组数据中的各个数减这组数据的平均数的平方和的平均数，如（1，2，3，4，5）这组数据的方差，就先求出这组数据的平均数（1+2+3+4+5）÷5＝3，然后再求各个数与平均数的差的平方和，用（1-3）?+（2-3）?+（3-3）?+（4-3）?+（5-3）?＝10，再求平均数10÷5＝2，即这组数据的方差为2

　　标准差

　　标准差给我们描述的是样本集合的各个样本点到均值的距离之平均

　　以这两个集合为例，[0, 8, 12, 20]和[8, 9, 11, 12]，两个集合的均值都是10，但显然两个集合的差别是很大的，计算两者的标准差，前者是8.3后者是1.8，显然后者较为集中，故其标准差小一些，标准差描述的就是这种“散布度”。之所以除以n-1而不是n，是因为这样能使我们以较小的样本集更好地逼近总体的标准差，即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。

　　方差和标准差的区别：

　　方差与我们要处理的数据的量纲是不一致的，多了个平方，虽然能很好的描述数据与均值的偏离程度，但是处理结果是不符合我们的直观思维的。 而标准差的根号就抵消了这个平方，就能相对直观了描述数据与均值之间的偏离程度。