{HCNA-AI 数学知识}之概率论内容介绍

3.1 概率论内容介绍

3.1.1 概率论介绍

概率论是研究随机现象数量规律的数学分支。随机现象是相对于决定性现象而言的，在一定条件下必然发生某一结果的现象称为决定性现象。

概率论是用来描述不确定性的数学工具，很多人工智能算法都是通过描述样本的概率相关信息或推断来构建模型。

3.1.2 实验介绍

本章节主要实现概率与统计相关的知识点，主要用到的框架是 numpy 和 scipy 框架。

3.2 概率论内容实现

提前导入模块，代码如下：

>>> import numpy as np

>>> import scipy as sp

3.2.1 均值实现

# 数据准备

>>> b = [1,3,5,6]

>>> ll = [[1,2,3,4,5,6],[3,4,5,6,7,8]]

# 代码输入：

>>> np.mean(b)

# 结果输出：

>>> 3.75

>>> np.mean(ll) #全部元素求均值

# 结果输出：

>>> 4.5

>>> np.mean(ll,0) #按列求均值

# 结果输出：

>>> [2. 3. 4. 5. 6. 7.]

>>> np.mean(ll,1) #按行求均值

# 结果输出：

>>> [3.5 5.5]

3.2.2 方差与标准差实现

# 数据准备

>>> b=[1,3,5,6]

>>> ll=[[1,2,3,4,5,6],[3,4,5,6,7,8]]

# 求方差：

# 代码输入：

>>> np.var(b)

# 结果输出：

>>> 3.6875

# 代码输入：

>>> np.var(ll[0])

# 结果输出：

>>> 3.6874999999999996

# 代码输入：

>>> np.var(ll,1)) #第二个参数为 1，表示按行求方差

# 结果输出：

>>> [2.91666667 2.91666667]

3.2.3 标准差实现

# 数据准备

>>> b=[1,3,5,6]

>>> ll=[[1,2,3,4,5,6],[3,4,5,6,7,8]]

# 代码输入：

>>> np.std(b)

# 结果输出：

>>> 1.920286436967152

# 代码输入：

>>> np.std(ll)

# 结果输出：

>>> 1.9790570145063195

3.2.4 协方差实现

# 数据准备

>>> b=[1,3,5,6]

# 代码输入：

>>> np.cov(b)

# 结果输出：

>>> 4.916666666666666

3.2.5 相关系数

# 数据准备

>>> vc=[1,2,39,0,8]

>>> vb=[1,2,38,0,8]

利用函数实现：

# 代码输入：

>>> np.corrcoef(vc,vb)

# 结果输出：

>>> 4.916666666666667

自定义实现：

# 代码输入：

>>> np.mean(np.multiply((vc-np.mean(vc)),(vb-np.mean(vb))))/(np.std(vb)*np.std(vc))

# 结果输出：

>>> 4.916666666666666

3.2.6 二项分布实现

服从二项分布的随机变量 X 表示在 n 次独立同分布的伯努利试验中成功的次数，其中每次试验的成功概率为 p。

# 代码输入：

from scipy.stats import binom, norm, beta, expon import numpy as np

import matplotlib.pyplot as plt

binom_sim = binom.rvs(n=10, p=0.3, size=10000) print('Data:',binom_sim)

print('Mean: %g' % np.mean(binom_sim)) print('SD: %g' % np.std(binom_sim, ddof=1)) plt.hist(binom_sim, bins=10, normed=True) plt.xlabel(('x'))

plt.ylabel('density') plt.show()

# 结果输出：

Data: [2 4 3 ... 3 4 1]

Mean: 2.9821

SD: 1.43478

# 分布图如下：

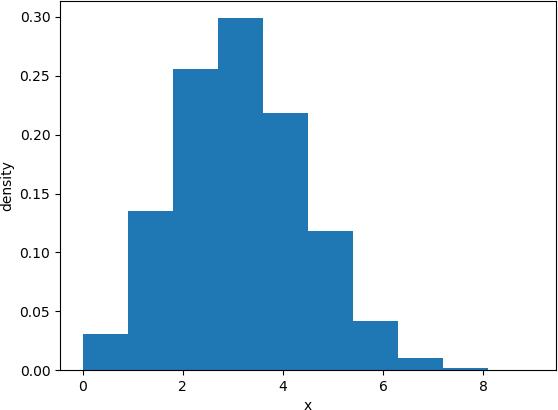
3.2.1 泊松分布实现

一个服从泊松分布的随机变量 X，表示在具有比率参数λ的一段固定时间间隔内，事件发生的次数。参数λ告诉你该事件发生的比率。随机变量 X 的平均值和方差都是λ。

# 代码输入：

import numpy as np

import matplotlib.pyplot as plt

x = np.random.poisson(lam=5, size=10000) pillar = 15

a = plt.hist(x, bins=pillar, normed=True, range=[0, pillar], color='g', alpha=0.5) plt.plot(a[1][0:pillar], a[0], 'r')

plt.grid() plt.show()

# 分布图如下：

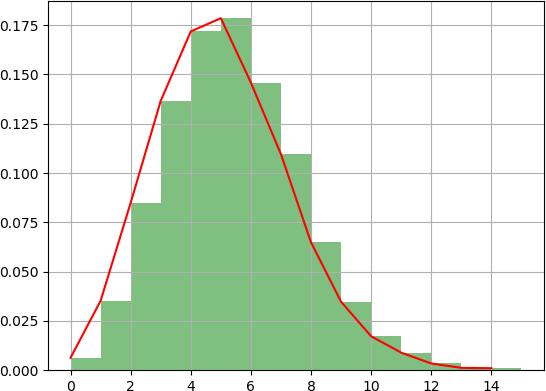
注：该代码只在可视化界面下才能输出上述图形，学员可在自己本地环境下测试。

3.2.1 正态分布

正态分布是一种连续分布，其函数可以在实线上的任何地方取值。正态分布由两个参数描述： 分 布 的 平 均 值 μ 和 标 准 差 σ                                                                                                                   。# 代码输入：

from scipy.stats import norm import numpy as np

import matplotlib.pyplot as plt

mu = 0

sigma = 1

x = np.arange(-5, 5, 0.1)

y = norm.pdf(x, mu, sigma) plt.plot(x, y)

plt.xlabel('x') plt.ylabel('density') plt.show()

# 分布图如下：

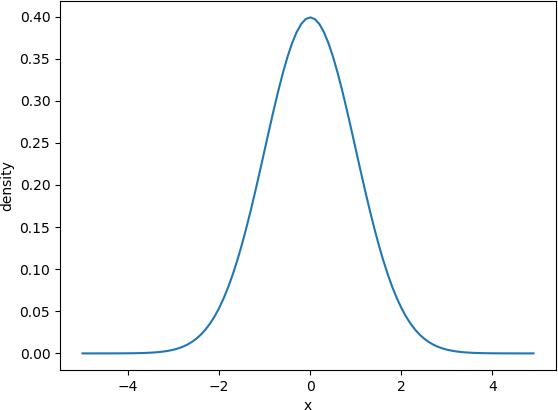
注：该代码只在可视化界面下才能输出上述图形，学员可在自己本地环境下测试。

3.2.1 beta 分布

beta 分布是一个取值在 [0, 1] 之间的连续分布，它由两个形态参数α和β的取值所刻画。

# 代码输入：

from scipy.stats import beta import numpy as np

import matplotlib.pyplot as plt

a = 0.5

b = 0.5

x = np.arange(0.01, 1, 0.01) y = beta.pdf(x, a, b) plt.plot(x, y)

plt.title('Beta: a=%.1f,b=%.1f' % (a, b)) plt.xlabel('x')

plt.ylabel('density') plt.show()

# 分布图如下：

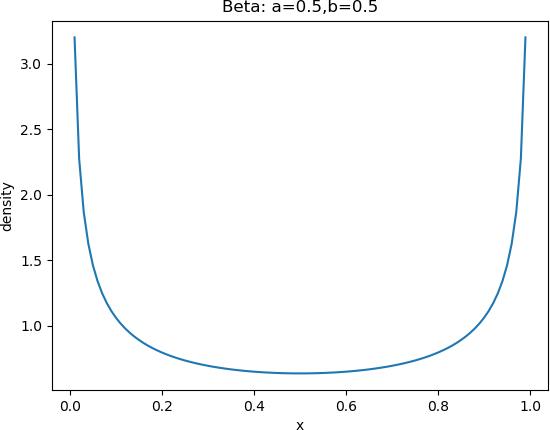
注：该代码只在可视化界面下才能输出上述图形，学员可在自己本地环境下测试。

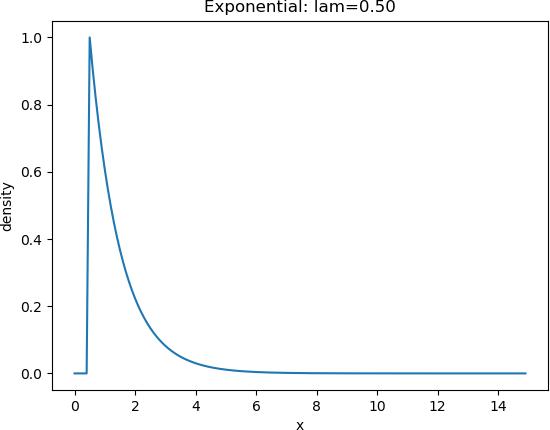
3.2.1 指数分布

指数分布是一种连续概率分布，用于表示独立随机事件发生的时间间隔。比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔等。

# 代码输入：

from scipy.stats import expon import numpy as np

import matplotlib.pyplot as plt

lam = 0.5

x = np.arange(0, 15, 0.1) y = expon.pdf(x, lam) plt.plot(x, y)

plt.title('Exponential: lam=%.2f' % lam) plt.xlabel('x')

plt.ylabel('density') plt.show()

# 分布图如下：

注：该代码只在可视化界面下才能输出上述图形，学员可在自己本地环境下测试​