机器学习之朴素贝叶斯算法(上)
1.算法概述
在机器学习中,有许多算法,大致可以分成分类算法和回归算法,分类算法有K近邻、朴素贝叶斯、决策树、随机森林、逻辑回归、神经网络等等,回归算法有线性回归、岭回归等等。朴素贝叶斯算法作为分类算法之一,它简单高效,在处理分类问题上,是应该首先考虑的方法之一。
本篇文章主要是介绍朴素贝叶斯算法涉及到的数学知识概率论相关知识
2.随机试验
满足以下三个特点的试验称为随机试验:
–可以在相同的条件下重复进行。
–每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果。
–进行一次试验之前不能确定哪一个结果会出现。
举例:
–E1:抛两枚硬币,出现正面H、反面T的情况。
–E2:抛一枚骰子,观察可能出现的点数情况。
3.样本点、样本空间、随机事件
样本点(sample point):随机试验的每一个可能的结果称为样本点,用e表示。
样本空间(sample space):随机试验E的所有可能结果组成的集合,记作S,即S={e1,e2,…,en }.
随机事件(random variables events ):样本空间S的任一子集A。属于事件A的样本点出现,则称事件A发生。特别的,仅含一个样本点的随机事件,称为基本事件。
举例:
随机试验:抛一枚骰子,观察可能出现的点数情况。
样本空间为:S={1,2,3,4,5,6}
样本点为:ei=1,2,3,4,5,6.
随机事件A1:“骰子出现的点数为5”,即A1={x│x=5}
4.随机变量
随机变量(random variable): 表示随机试验各种结果的实值单值函数。
举例1:随机试验:抛两枚骰子,观察可能出现的点数的和。试验的样本空间是S={e}={(i,j)|i,j=1,2,3,4,5,6},i,j分别是第1次,第2次出现的点数,以X记为两球号码之和,则X是一个随机变量。
X=X(e)=X(i,j)=i+j,i,j=1,2,?,6.
?举例2:随机试验E1:抛两枚硬币,出现正面??、反面??的情况。试验的样本空间是S={HH,HT,TH,TT},以Y记为两次投掷硬币得到反面T的总数,则Y是一个随机变量。
5.概率与条件概率
贝叶斯算法是基于条件概率的一种算法,接下来我们先理解一下概率及条件概率的概念。
概率亦称“或然率”。它反映随机事件出现的可能性(likelihood)大小。随机事件是指在相同条件下,可能出现也可能不出现的事件。例如,从一批有正品和次品的商品中,随意抽取一件,“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察,其中A事件出现了m次,即其出现的频率为m/n。经过大量反复试验,常有m/n越来越接近于某个确定的常数(此论断证明详见伯努利大数定律)。该常数即为事件A出现的概率,常用P (A) 表示。
条件概率,是指事件A在另外一个事件B已经发生条件下的发生概率
在很多情况下,我们感兴趣的是某个事件在给定其他事件发生时出现的概率,这种概率叫做条件概率:
P(Y│X)=(P(YX))/(P(X))
联合概率, 是指在多元的概率分布中多个随机变量分别满足各自条件的概率。假设X和Y都服从正态分布,那么P{X<4,Y<0}就是一个联合概率,表示X<4,Y<0两个条件同时成立的概率。表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B),或者P(A∩B)
例如有以下样本数据
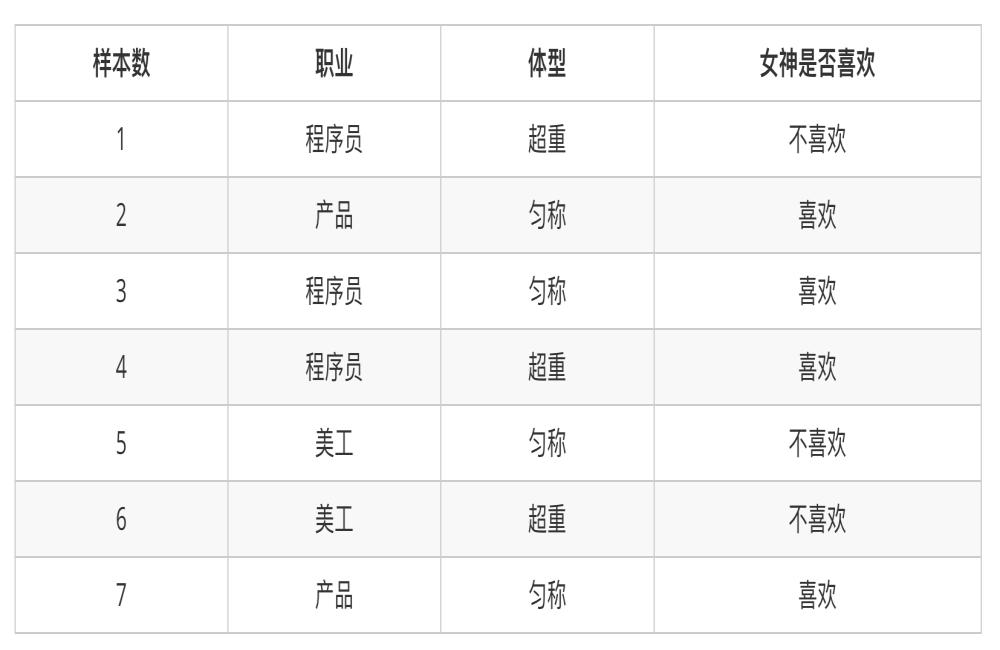
问题:
1、女神喜欢的概率?
2、职业是程序员并且体型匀称的概率?
3、在女神喜欢的条件下,职业是程序员的概率?
4、在女神喜欢的条件下,职业是产品,体重是超重的概率?
分析以上样本数据,得出来的答案如下:
1、女神喜欢的概率?
此题属于概率问题,女神喜欢的有4个样本数据,不喜欢的有3个样本数据,所以女神喜欢的概率是 4/7
2、职业是程序员并且体型匀称的概率?
此题属于联合概率问题,职业是程序员的概率是3/7,体型匀称是4/7,因此,职业是程序员并且体型匀称的概率是3/7*4/7=12/49
3、在女神喜欢的条件下,职业是程序员的概率?
此题属于条件概率问题,女神喜欢的有4个数据样本,在女神喜欢的条件下,职业是程序员的概率2/4
4、此题属于联合概率问题,按联合概率对此问题可以进行分解
P(女神喜欢|(职业是产品,体重是超重))=P(女神喜欢|职业是产品∩女神喜欢|职业是程序员)=1/4*1/2=1/8
此篇文章主要是介绍朴素贝叶斯算法的概率基础,下一篇文章将会介绍朴素贝叶斯算法原理及相关案例。


